Jumping on the Clouds:
Emma is playing a new mobile game involving n clouds numbered from 0 to n-1 A player initially starts out on cloud \(c_0\) , and they must jump to cloud \(c_n-1\) In each step, she can jump from any cloud i to cloud i+1 or cloud i+2 There are two types of clouds, ordinary clouds and thunderclouds. The game ends if Emma jumps onto a thundercloud, but if she reaches the last cloud (i.e.,\(c_n-1\)) she wins the game!

Can you find the minimum number of jumps Emma must make to win the game? It is guaranteed that clouds \(c_0\) and \(c_n-1\) are ordinary-clouds and it is always possible to win the game.
Input Format
The first line contains an integer, n (the total number of clouds). The second line contains n space-separated binary integers describing clouds \(c_0\) ,\(c_1\),….\(c_n-1\)
- if \(c_i\)=0 , the \(i^{th}\) cloud is an ordinary cloud.
- if \(c_i\)=1 , the \(i^{th}\) cloud is a thundercloud.
Output Format
Print the minimum number of jumps needed to win the game.
Constraints:
- 2<=n <=100
- \(c_i\) E{0,1}
- \(c_0\) = \(c_n-1\)=0
Sample Input 0
7
0 0 1 0 0 1 0
Sample Output 0
4
Sample Input 1
6
0 0 0 0 1 0
Sample Output 1
3
Explanation
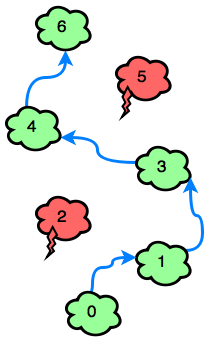
Sample Case 0: Because \(c_2\) and \(c_5\) in our input are both 1 , Emma must avoid \(c_2\) and \(c_5\) . Bearing this in mind, she can win the game with a minimum of 4 jumps:
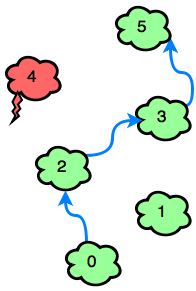
Sample Case 1: The only thundercloud to avoid is \(c_4\) . Emma can win the game in 3 jumps:
Solution
#!/bin/python
import sys
n = int(raw_input().strip())
c = map(int,raw_input().strip().split(' '))
c.insert(n,0)
count = 0
i = 0
while (i < n-1):
i += (c[i+2] == 0)+1
count += 1
print count

